If/else statements allow you to create a code segment that has checks. If/ElseIf/Else statments can be used to decide different program outputs depending on what the user inputted. Switch statements are also an alternative method to if statements.

Conditionals Exercises 1-20 Even

// Exercise 2
int a = 1;
int b = 5;
int c = 1;
double d = Math.pow(b,2) - 4 * a * c;
if (d > 0) {
    double root1 = (-b + Math.sqrt(d)) / (2 * a);
    double root2 = (-b - Math.sqrt(d)) / (2 * a);
    System.out.println(root1);
    System.out.println(root2);
} else {
    System.out.println("not real");
}

-0.20871215252208009
-4.7912878474779195

// Exercise 4
float blah = 25;

if (blah == 0) {
    System.out.println("zero");
}
else if (blah > 0) {
    System.out.println("positive");
} else {
    System.out.println("negative");
}
if (Math.abs(blah) < 1 ) {
    System.out.println("small");
}
if (Math.abs(blah) > 1000000 ) {
    System.out.println("big");
}

positive

// Exercise 6
import java.util.Scanner;
Scanner in = new Scanner(System.in);

System.out.print("Input floating-point number: ");
double x = in.nextDouble();
System.out.print("Input floating-point another number: ");
double y = in.nextDouble();

x = Math.round(x * 1000);
x = x / 1000;

y = Math.round(y * 1000);
y = y / 1000;

if (x == y)
{
    System.out.println("They are the same up to three decimal places");
}
else
{
    System.out.println("They are different");
}

Input floating-point number: Input floating-point another number: They are different

// 8
import java.util.Scanner;
Scanner in = new Scanner(System.in);

System.out.print("Input an alphabet: ");
String input = in.next().toLowerCase();

boolean uppercase = input.charAt(0) >= 65 && input.charAt(0) <= 90;
boolean lowercase = input.charAt(0) >= 97 && input.charAt(0) <= 122;
boolean vowels = input.equals("a") || input.equals("e") || input.equals("i")
        || input.equals("o") || input.equals("u");

if (input.length() > 1)
{
    System.out.println("Error. Not a single character.");
}
else if (!(uppercase || lowercase))
{
    System.out.println("Error. Not a letter. Enter uppercase or lowercase letter.");
}
else if (vowels)
{
    System.out.println("Input letter is Vowel");
}
else
{
    System.out.println("Input letter is Consonant");
}

Input an alphabet: Input letter is Consonant

// 10
int i;
System.out.println ("The first 10 natural numbers are:\n");
for (i=1;i<=10;i++)
{      
    System.out.println (i);
}
System.out.println ("\n");

The first 10 natural numbers are:

1
2
3
4
5
6
7
8
9
10

// 12
import java.util.Scanner;

int i,n=0,s=0;
double avg;
{
    
    System.out.println("Input the 5 numbers : ");  
        
}
    for (i=0;i<5;i++)
    {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        
    s +=n;
}
avg=s/5;
System.out.println("The sum of 5 no is : " +s+"\nThe Average is : " +avg);

Input the 5 numbers : 
The sum of 5 no is : 34
The Average is : 6.0

// 14
import java.util.Scanner;

int j,n;

System.out.print("Input the number(Table to be calculated): ");
{
System.out.print("Input number of terms : ");
Scanner in = new Scanner(System.in);
        n = in.nextInt();

System.out.println ("\n");
for(j=0;j<=n;j++)

    System.out.println(n+" X "+j+" = " +n*j);
}

Input the number(Table to be calculated): Input number of terms : 

67 X 0 = 0
67 X 1 = 67
67 X 2 = 134
67 X 3 = 201
67 X 4 = 268
67 X 5 = 335
67 X 6 = 402
67 X 7 = 469
67 X 8 = 536
67 X 9 = 603
67 X 10 = 670
67 X 11 = 737
67 X 12 = 804
67 X 13 = 871
67 X 14 = 938
67 X 15 = 1005
67 X 16 = 1072
67 X 17 = 1139
67 X 18 = 1206
67 X 19 = 1273
67 X 20 = 1340
67 X 21 = 1407
67 X 22 = 1474
67 X 23 = 1541
67 X 24 = 1608
67 X 25 = 1675
67 X 26 = 1742
67 X 27 = 1809
67 X 28 = 1876
67 X 29 = 1943
67 X 30 = 2010
67 X 31 = 2077
67 X 32 = 2144
67 X 33 = 2211
67 X 34 = 2278
67 X 35 = 2345
67 X 36 = 2412
67 X 37 = 2479
67 X 38 = 2546
67 X 39 = 2613
67 X 40 = 2680
67 X 41 = 2747
67 X 42 = 2814
67 X 43 = 2881
67 X 44 = 2948
67 X 45 = 3015
67 X 46 = 3082
67 X 47 = 3149
67 X 48 = 3216
67 X 49 = 3283
67 X 50 = 3350
67 X 51 = 3417
67 X 52 = 3484
67 X 53 = 3551
67 X 54 = 3618
67 X 55 = 3685
67 X 56 = 3752
67 X 57 = 3819
67 X 58 = 3886
67 X 59 = 3953
67 X 60 = 4020
67 X 61 = 4087
67 X 62 = 4154
67 X 63 = 4221
67 X 64 = 4288
67 X 65 = 4355
67 X 66 = 4422
67 X 67 = 4489

// 16
import java.util.Scanner;

int i,j,n;
System.out.print("Input number of rows : ");
Scanner in = new Scanner(System.in);
        n = in.nextInt();

for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
    System.out.print(j);

System.out.println("");
}

Input number of rows : 1
12
123
1234
12345

// 18
import java.util.Scanner;

int i,j,n,k=1;

System.out.print("Input number of rows : ");

Scanner in = new Scanner(System.in);
    n = in.nextInt();

for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
System.out.print(k++);
System.out.println("");
}

Input number of rows : 1
23
456

// 20
import java.util.Scanner;

int numberOfRows;
System.out.print("Input number of rows : ");
Scanner in = new Scanner(System.in);
        numberOfRows = in.nextInt();
int number = 1;
for (int row = 1; row <= numberOfRows; row++)
{
for (int column = 1; column <= row; column++)
    {
    System.out.print(number + " ");
    number++;
    }
    System.out.println();
}

Input number of rows : 1 
2 3 
4 5 6 
7 8 9 10 
11 12 13 14 15 
16 17 18 19 20 21 
22 23 24 25 26 27 28 
29 30 31 32 33 34 35 36 
37 38 39 40 41 42 43 44 45

Notes (courtesy of Bailey S)

Truth Tables

Truth tables can be used to visualize boolean conditionals. They're useful for evaluating basic boolean expressions as well as more complicated compound boolean expressions, which use multiple kinds of boolean operators inside each other.

De Morgan's Law

De Morgan's Law is a bit more mathematical in nature, dealing with set theory, so I'll try my best to describe it here.

De Morgan's Law basically explains how certain boolean statements can be rewritten as different expressions, yet essentially be the same. More specifically, it states that "The complement of the union of two sets is the same as the intersection of their complements" or "The complement of the intersection of two sets is the same as the union of their complements".

What the heck does that mean? An easier way to think about it would be like this:

not (A or B) = (not A) and (not B)
not (A and B) = (not A) or (not B)

In a more formalalized, mathematical way:

Set Theory Stuff

But even with all that text, it's still pretty confusing, right? So it's probably best to visualize it using an actual image. This one I found online pretty much summarizes it best:

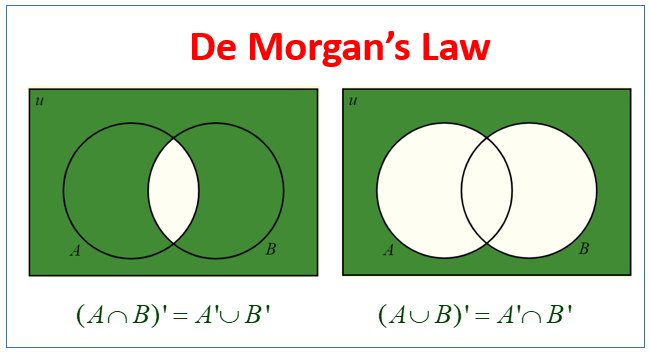
More Set Theory Stuff

The green shaded area is basically what's being covered in each equality. Both sides cover the same thing.

Finally, let's go through an example of how this would apply in code. Essentially, we'll use a few variables to make a whole bunch of complicated compounded boolean expressions that actually mean the same exact thing: